With the series of articles on zero-knowledge proofs (ZKPs), I’m aiming to create a guide on their practical applications that will be helpful for fellow software engineers interested in the topic. The first article will cover the path from my initial fascination with ZKPs to my understanding of ZKP application architecture basics.
What Are The Zero-Knowledge Proofs?
ZKPs are genuinely fascinating. Before learning about them, I used to think of cryptography merely as a means of secure communication, where Alice needs to pass some information to Bob in a way that only prevents any other party from learning it. However, ZKP blew my mind by stating that Alice may convince Bob that she knows some information without passing any of it to Bob. Zero-knowledge cryptography has been evolving since the 1980s, but it has only recently reached a production-ready stage from an engineering perspective. It opens up entirely new possibilities, like:
- Proving that you know your password without it leaving your machine (even in encrypted form);
- Proving that your bank account balance is above a certain amount without disclosing the actual amount;
- Proving to a recommendation algorithm that you really like this kind of content or are interested in this kind of ad without letting it know any of your personal data;
and many others of which we’re not yet aware. Speaking more formally, a zero-knowledge proof is a method by which one party (the prover) can prove to another party (the verifier) that a given statement is true without revealing any additional information apart from the fact that the statement is indeed true. Such cryptographic “black magic” challenged my curiosity enough for me to wish to understand how it works and try it in practice.
From Theory To Practice
While choosing my first ZK project, I was initially inspired by this Mastermind ZKP implementation to find some incomplete information games that could benefit from ZKPs. In the case of Mastermind, ZKPs solve the trust issue between the game master and the code breaker in the same way the physical board setup solves it in the original game. Once the game master inserts the four colored pegs, she cannot change the configuration. When the game round ends, the code breaker can inspect the initial setup and verify that the game master did not cheat. One of the “brilliant” ideas that almost immediately came to my mind was Battleship - the game I immensely enjoyed as a kid.
Similarly to Mastermind, fixing the initial ship locations on paper solves the trust issue, and players can check each other’s setup at the end to verify that the other party is honest. However, to my surprise, I discovered several different ZK implementations of Battleship and decided to move on to a different idea. “Proof” in “zero-knowledge proof” made me think of games where you need to prove something to another party, and a recently viral one came to my mind.
Hello, ZK-Wordle!
Probably everyone knows Wordle. The hardcore players also know that the list of words is publicly available, the word of the day is not chosen at random (surprised?), and all the game code lives in your browser, so it’s not that difficult to cheat. Moreover, the social sharing feature is merely a copy-paste of plaintext game stats that a player can edit. So every day, on 0:01:01, I could tweet
Wordle 396 1/6
🟩🟩🟩🟩🟩
and be the absolute Wordle world champion in others' eyes (feel free to copy this one, too: 🟩). But obviously, everyone is playing Wordle for the challenge and for the fun of guessing by looking at others' clue patterns. So the number of cheaters is probably around 2% (yes, there is a study for that). Anyway, my purpose with this project was to understand how to apply ZKPs in the real world. So let’s pretend that proving that your Wordle game stats are accurate is a severe problem that demands a cryptographically strong solution for the rest of the article.
Solving The Trust Issues
At first, I was misled by the meaning of proof in the context of Wordle. Typically, players prove to others that they solved the daily puzzle by posting the clue patterns on social media. So my initial idea was to generate and share a ZK proof along with the clues. Without going into the technical details of what a ZK proof looks like, let’s assume that we have a magic function, f, that returns true if a given clue represents the correct relation between guess and solution according to the rules of Wordle, and false otherwise.
f(guess,solution,clue) == true.
E.g., if the answer was “start” and the guess was “spear,” the clue looking like 🟩 ⬜ ⬜ 🟨 🟨 would be proven valid.
Unfortunately, this solves the “faked stats sharing” problem only if we trust the proving player not to modify the solution. However, the original game code, including picking the word of the day, is loaded entirely in the user’s browser. So, if I’m willing to cheat, there is no way to ensure that I didn’t run something else through the proof on my side, like
f("smart","smart","🟩🟩🟩🟩🟩") == true.
So how do we fix the solution to make the game fair for everyone? The problem is starting to look like a multiplayer game, and a typical multiplayer game has a server to which everyone connects. Creating a backend service to fetch the word of the day that is the same for everyone would solve the problem. However, getting the solution from the server still does not prevent me from replacing it with something else before running it through the “magic proving function” f. At this point, I realized that regardless of whom we expect to prove something about their Wordle game results, in ZKP, the prover is always the one who knows all the inputs to the proving function f, including the secret ones. As soon as we move the word of the day choice server-side, the backend should become the prover! Sounds counter-intuitive? The backend service is the “game master,” so why should it prove anything to anyone? Well, precisely for the reason that we wish to create a fair game for everyone. This realization made me restructure the application in such a way that the backend service spits out the clue in response to the player’s guess and, at the same time, proves that this clue is valid. The game flow at this stage would look like the following:
- Player feeds the guess into the backend service;
- Backend service calculates the clue;
- Backend service generates the proof;
- Backend service sends proof and the clue back to the player.
Looks cumbersome? Luckily, the current ZK development tools allow us to prove whether some statement is true or false and simultaneously perform arbitrary calculations on the inputs. It simplifies the above algorithm as follows:
- Player feeds the guess into the backend service;
- Backend service generates the clue, at the same time proving that it’s correct;
- Backend service sends the proof containing the clue back to the player.
That’s much better - we don’t have to trust the player because the player never learns the solution until the backend reveals it at the end of the game round. Our proving function now looks like the following:
Proof{clue} = f(solution, guess).
Can we trust the backend, though? Imagine for a moment that the winner could receive a large cash prize - would the server owner resist the temptation to collude with some player and secretly reveal the word of the day to them to split the reward later? It turns out that there is a way to ensure that even the opaque backend service cannot cheat. This critical element of ZKP application architecture is called commitment.
Commitment For Trust
The Wiki says, “a commitment scheme is a cryptographic primitive that allows one to commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later.” So, how to publicly “fix” our word of the day without revealing it? One of the most straightforward commitment schemes is hashing. Our server can publicly reveal the solution hash at the beginning of a new game round. A public blockchain is naturally the best place to do that since it is immutable. At the end of the round, the server can reveal the original solution, and everyone can check that the server indeed derived the hash from that solution. Is there a way to ensure that the server used the same solution it hashed during the proving process inside f? For this purpose, we need to include the hash check inside our proof. Our proving function would look like the following:
Proof{clue} = f(solution, guess, solutionHash).
Inside it, we generate the clue output (🟩 ⬜ ⬜ 🟨 🟨) and check that hash(solution) == solutionHash. Now, our players can trust the backend “game master” with the solution. As it turns out, ZKPs and public commitment schemes are a combination powerful enough to enable MMO games where an entire game world is committed on-chain.
So far, we’ve regarded the generated proof as always valid, but how do we actually check it?
Trust, But Verify
Proof verification is an essential mechanism of ZKPs. The generated proof alone doesn’t help players trust the backend or any player to trust each other. Let’s see how ZKPs provide a way to verify that the proof is valid and that the one who generated it indeed used the intended proving function f.
Every ZKP scheme has a corresponding algorithm for proof verification. Besides the proof, the algorithm requires some input parameters specific to the proving function f. Anyone who knows the proving function f can generate those parameters for the verification algorithm. It makes the verification process reproducible, meaning that in theory, not only the original verifier can carry it out, but anyone who knows the proving function f. In practice, some ZKP schemes have a so-called trusted setup phase necessary for the verification parameters generation. It involves multiple parties, thus making the parameters generation a one-off event. However, the parties involved are usually the ones who are interested in each other’s fairness (e.g., a prover and a verifier), and the setup phase protocol helps to resolve the trust issue.
We’ll leave the technical details of verification for the following article, but what’s interesting for us to know now is that there is a way to generate the verifier program in the form of a smart contract. Such a smart contract would already contain function-specific parameters and have a verifying function that accepts the proof and returns true or false depending on the proof’s validity. On-chain verification allows anyone to carry it out permissionless, and neither the backend nor the player is responsible for hosting the verification code. In our case, we should let the player verify the proof coming from the backend to be sure that every clue is correct. We should also let players verify each other’s proof of the shared game stats. Note that the stats only show that this particular player indeed made the guesses that resulted in the corresponding colored clue patterns. It doesn’t prevent players from cheating by playing multiple game sessions, but neither does the original game (anyone can start as many private browsing sessions as necessary to beat it). Proving that a player has played only once requires introducing some identity system that makes it costly to create new identities, which is a non-trivial task out of the scope of our exploration of ZKPs. With that said, we can finalize our ZK-Wordle app architecture.
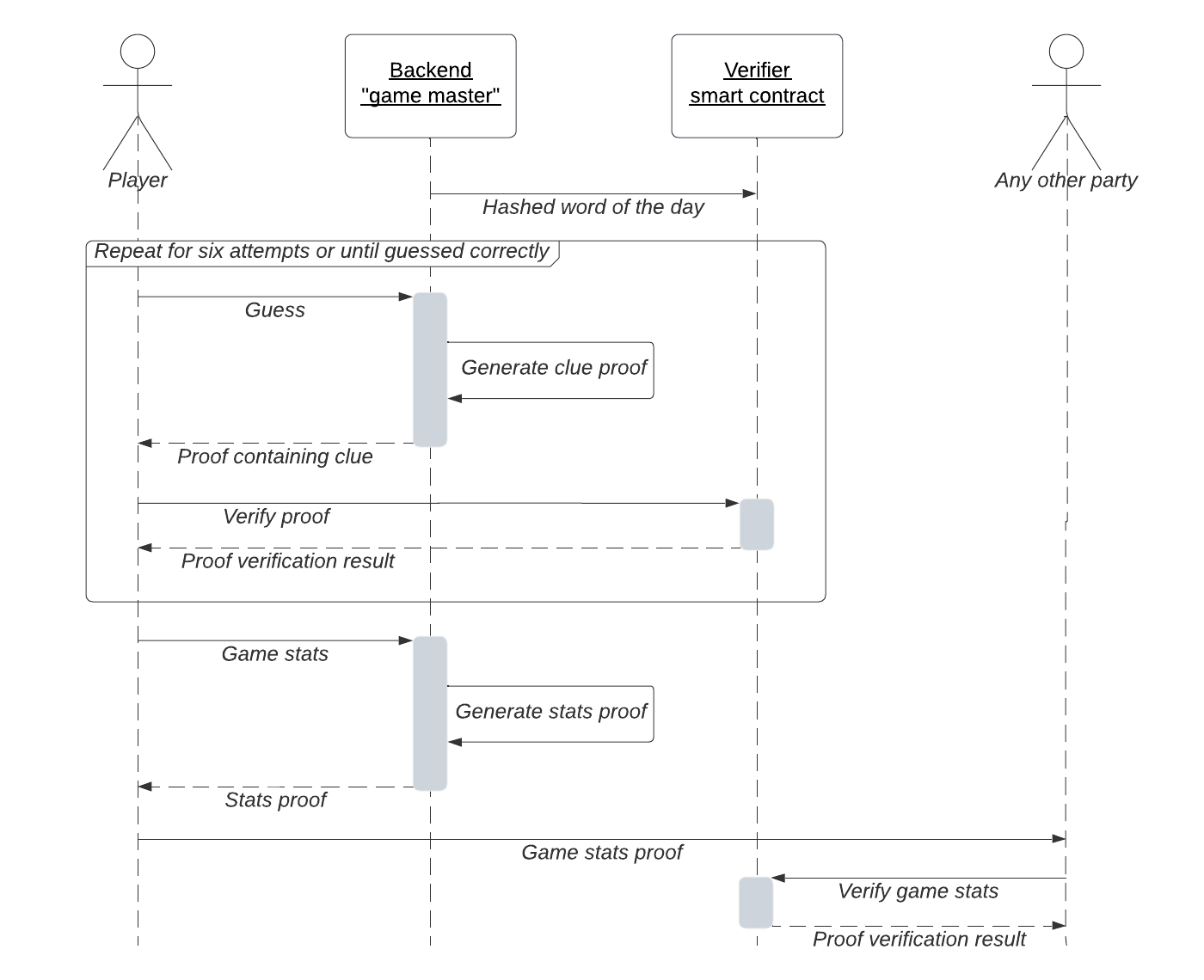
As presented in the diagram above, our ZK-Wordle app should operate the following way:
- At the beginning of the day, the backend server secretly picks the word of the day (solution) and openly commits its hash on a public blockchain.
- During the game round, the player feeds guesses into the backend service.
- Backend service generates the ZK-proof containing the clue and checks that the solution hash is the same as the publicly committed one in the process.
- Backend service sends the proof containing the clue back to the player.
- Player learns the clue and uses the smart contract to verify the proof.
- At the end of the round, the player can request the backend to generate the stats proof and share it with other players.
- Other players can verify the shared stats proof using the smart contract.
Conclusion
In the article, I presented some essential concepts of zero-knowledge proofs behind the architecture of a ZKP-enabled Wordle game. Let’s quickly summarize them:
- In any ZK application, the prover must know all the inputs, including the secret ones. The verifier will never learn them but can trust the prover’s output because of the underlying cryptography of the ZK verification protocol.
- Commitment schemes play an essential role in ZK applications. They ensure that the private inputs stay the same for every generated proof without revealing them.
- Public blockchains, with their immutability and permissionless nature, are extremely helpful for ZK applications. They appear to be among the best places to host commitments and proof verification algorithms.
You can find the project source code in this GitHub repository. The following article will detail how the zero-knowledge proofs are described in the program code and will put together the architectural pieces we outlined here.
I want to give special thanks to Chih Cheng Liang and James Murdza for their valuable feedback.